시리즈물로 제작 중입니다. 이전 내용과 이어집니다.
https://songmin9813.tistory.com/5(4. Picoke)
5. Twigitizer
1. 싱글 플레이 게임 기획 의도
우리 프로젝트가 다른 서비스에 비해 차별성을 가지는 항목 단 한 가지를 꼽자면 ‘사용자하고의 상호작용’을 들 수 있겠다. 이는 즉 멀티 플레이 게임을 상정하고 게임을 만들어야 함을 의미한다.
이와 관련된 기획 회의를 팀원/멘토들과 진행을 초창기 때 꽤나 많이 했던 것 같다. 여러 멘토에게 피드백을 받은 내용 중 가장 기억에 남은 내용이 있었는데, 이는 다음의 내용과 같았다.
와이프가 있는 저 같은 경우에는 다른 사람의 상호작용을 그렇게 원하지는 않을 것 같은데요…
이를 조금 더 확장/다듬어 말하게 되면 다음과 같은 경우 또한 처리할 수 있어야 함을 의미했다.
💡 상호작용을 원하지 않음, 통신의 오류, 메이트의 무응답, 도중 강제 종료 등 상호작용 자체가 성립이 되지 않았을 때 필요한 기능/게임이 필요하다.
Maestro 기간 동안 정말 많은 게임과 더불어 여러 사람들을 만나면서 얻을 수 있는 인사이트 또한 무시할 수 없었다. 실제로도 우리 팀원들이 모두가 납득이 되는 이유였고, 이러한 이유로 ‘상호작용’이 두드러지는 우리의 서비스에 최소한의 싱글 플레이 게임을 넣어보자!라는 결과로 이어지게 된다.
사실 혼자서 할 수 있는 미니게임은 정말 많이 존재한다. 마음만 먹으면 ox문제, 지뢰 찾기, 계산 문제 등 메커니즘 자체를 그대로 따오는 방식으로 게임을 제작할 수도 있었다.
실제로 관련 코드와 API도 제공하는 것을 확인했지만, 기존 게임 메커니즘을 살짝만 비틀어서 구조적으로는 경험해보았지만 쉽게 경험해본 적이 없는 규칙을 만들어보는 것은 어떨까? 라는 생각이 문득 들었다.
전에 만든 게임은 이미지를 기반으로 해왔던 게임이기에 공학적/수학적인 느낌보다는 감각적인 느낌이 더 강하다. 이는 추후에 감각적인 느낌의 게임이 다수 만들어질 예정과도 같았기에 공학적인 게임을 한 번 만들어볼까…?라는 것이 계산기에 기반한 게임을 만들기로 한 결정적인 계기가 되었다.

계산기 게임이라고 하면 말그대로 계산기에 존재하는 수식들을 이용하여 원하는 결과를 도출해내는 게임을 통칭한다. 이를 피봇팅 한 게임으로는 아래와 같은 내용의 게임들을 여럿 봤던 것 같다.
- 수식의 결과가 그대로 누적 점수가 되는 것(상기 텐텐의 미니게임)
- 제한된 숫자들을 이용하여 특정한 결과를 만들어야 하는 게임(다빈치 코드)
- 수식에 빈 칸이 존재하고, 그 안에 숫자를 집어넣어 수식을 성립시켜야 하는 게임
등등…여러 게임과 그 메커니즘을 조사해보았을 때, 다음과 같은 공통점을 발견할 수 있었다.
💡 입력으로 0~9의 숫자, 또는 특정 숫자를 연산의 과정으로 입력해야 한다는 것
이러한 공통점을 뽑아냈다면 본인은 또 이렇게 피봇팅을 해본다.
💡 그렇다면 입력으로 연산의 과정이 아닌 연산의 결과만을 입력해야 하는 건?
간단하다 못해 발칙하게 시작된 피봇팅은 이후 만들어진 Tiwigitizer 게임의 주요한 뼈대가 되었다.
2. 게임의 구성

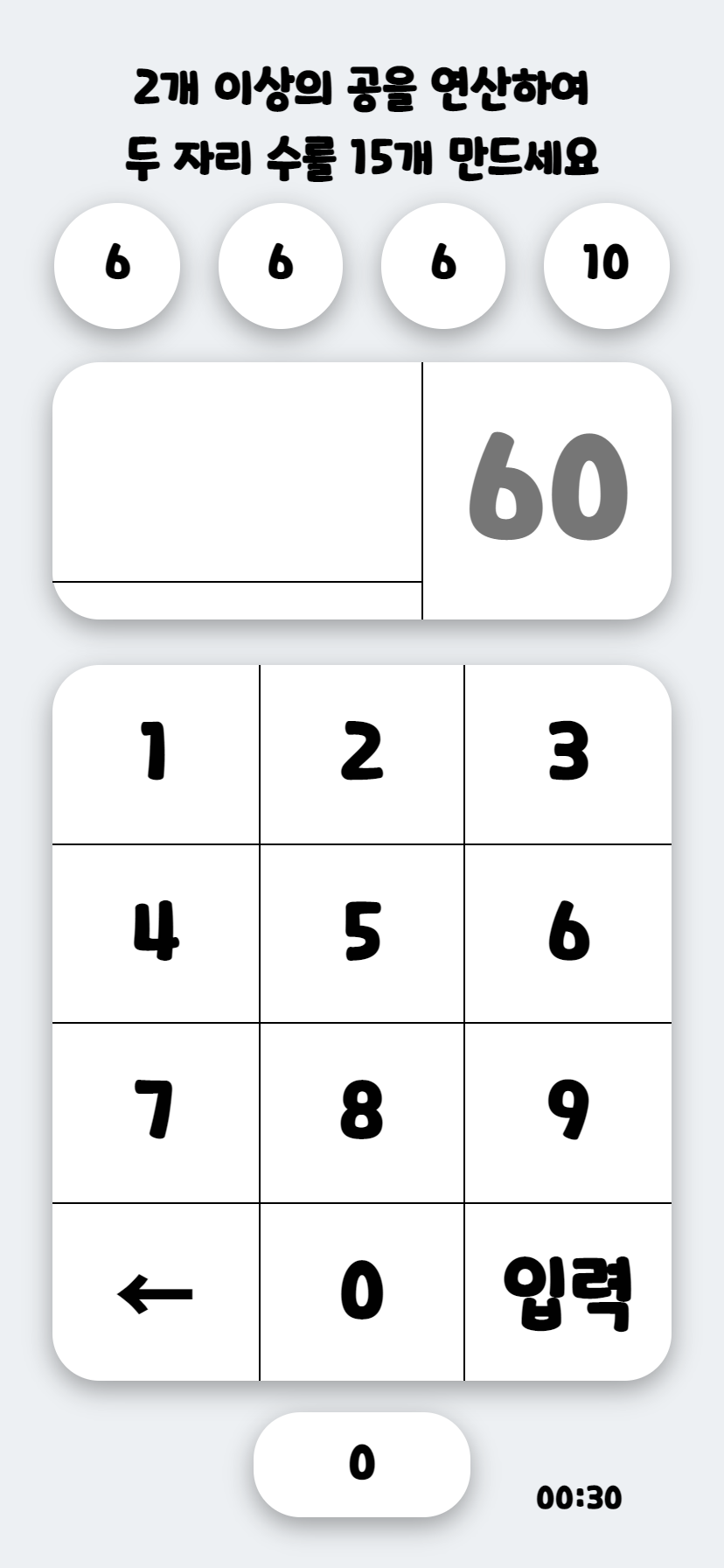
초기로 기획한 게임은 4개의 랜덤 숫자를 사칙연산하여 만들 수 있는 두 자릿수를 가능한 한 입력해야 하는 게임이다. 하지만 여기서 포인트는 계산기를 두드리는 과정에서 사칙연산은 전혀 들어가지 않고, 연산의 정답만을 입력하게 한다는 점이다.
게임의 이름은 ‘2개 이상의 공’이라는 뜻을 내포하고 있는 Twin과 계산기의 입력부가 마치 디지타이저(Digitizer)를 연상시키는 것 같아 이 둘을 합쳐 ‘Twigitizer(트위지타이저)’라는 이름을 붙이게 되었다.
이러한 게임을 만들기 위해서 게임은 네 자리 수를 이용한 모든 경우의 두 자릿수 연산 결과를 알아야 할 필요가 있었고, 이는 백트래킹을 이용한 DFS를 이용하여 구현하였다.
해당 로직을 이용하여 모든 경우의 수를 체크해본 결과 최소 3~40개, 평균적으로 60개 정도의 정답이 나오는 것을 확인하였다. 존재할 수 있는 두 자리 수가 10~99까지 90개인 것을 감안하면 쉬우면서도 1씩 수를 올리면서 찍기에는 살짝 부담이 되는 경우인 것 같아 해당 게임성을 가져도 충분할 것이라는 판단을 하였다.

1씩 더해가면서 문제를 푸는 어뷰징을 방지하기 위해 틀리거나 중복된 답안을 작성하였을 경우, 최초 5초 잠금-10초 잠금-15초 잠금-최대 20초 화면 잠금이라는 시스템을 도입하였다.
이는 내부 테스트 결과 처음 1~2번 정도는 실수로 입력할 수 있는 상황이 종종 발생하여 선택한 점진적 잠금 시스템이기도 하다.
혹시나 모든 경우의 수가 적어 문제 풀이에 부담이 될 수도 있을 것 같아 총 맞춰야 하는 개수를 다음과 같이 보정하는 작업을 포함하였다.
모든 답의 개수가 40개를 넘지 않는다면, 그 절반의 수로 문제 수를 대체해 줘!
const objCases = Math.min(20, Math.ceil(allCases.size / 2)); //cases correction
아무리 운이 좋지 못해도 절반 이상은 맞아야 문제를 풀 수 있도록 게임의 밸런스를 조정하였다.
3. 핵심 알고리즘(재귀 백트래킹+DFS)
사실 멀티 플레이보다 싱글 플레이가 제약사항을 프로그램이 만들어야 한다는 점에서 개발 난이도가 다른 게임에 비해 꽤 높았던 것 같다. 그 이유를 반증하 듯 사소한 예외 처리를 하면서 시간을 꽤 잡아먹었고, 해당 로직을 어떻게 구현할지에 대한 생각도 다른 게임에 비해 많은 시간을 들였다.
아래는 1. 네 자리 수가 배치되는 모든 경우의 수를 백트래킹을 이용하여 구현한 코드이다.
//let objNums=[ball_one, ball_two, ball_three, ball_four];
let visited = [false, false, false, false];
const currentNums = [];
const makeAllNumCases = (length, visited) => {
//using backtracking
if (length == objNums.length) {
//objective complete
makeAllCasesFromOrdering(currentNums);
return;
}
for (let i = 0; i < objNums.length; i++) {
if (!visited[i]) {
visited[i] = true;
currentNums.push(objNums[i]);
makeAllNumCases(length + 1, visited);//recursive call
currentNums.pop();
visited[i] = false;
}
}
};
다음 코드는 2. 1에서 만들어진 배열을 기반으로 스택을 이용한 DFS를 이용하여 모든 경우의 사칙 연산 결과를 저장하는 코드이다.
const makeAllCasesFromOrdering = (ordering) => {
//DFS logic using stack
orderingException(ordering);
const [a, b] = [ordering[0], ordering[1]];
//어려운 js의 세계.
const stack = [];
stack.push([`${a}+${b}`, "+", 2]);
stack.push([`${a}-${b}`, "-", 2]);
stack.push([`${a}*${b}`, "*", 2]);
if (a % b == 0) stack.push([`${a}/${b}`, "/", 2]);
while (stack.length != 0) {
const [fullOps, op, length] = stack.pop(); //비구조화^^
if (eval(fullOps) > 0 && String(eval(fullOps)).length == 2) {
if (tutorialCode.length != 6) tutorialCode.push(eval(fullOps));//making tutorial
if (
!allCases.has(eval(fullOps)) ||
(allCases.has(eval(fullOps)) &&
allCases.get(eval(fullOps)).length > fullOps.length)//exception case
)
allCases.set(eval(fullOps), fullOps);
}
if (length == ordering.length) continue; //exception case
stack.push([`${fullOps}+${ordering[length]}`, "+", length + 1]); //plus op
stack.push([`${fullOps}-${ordering[length]}`, "-", length + 1]); //minus op
if (op == "+" || op == "-")
stack.push([`(${fullOps})*${ordering[length]}`, "*", length + 1]);
//multiple op
else stack.push([`${fullOps}*${ordering[length]}`, "*", length + 1]);
if (eval(fullOps) % ordering[length] == 0) {
//divide op
if (op == "+" || op == "-")
stack.push([`(${fullOps})/${ordering[length]}`, "/", length + 1]);
else stack.push([`${fullOps}/${ordering[length]}`, "/", length + 1]);
}
}
};
로직의 작동 방식은 랜덤으로 선택된 4개의 숫자의 모든 배치 순서에 대한 모든 사칙 연산 결과를 저장하는 방식으로 작동케 했다.
예전에 백준 문제에서 백트래킹 문제들과 비슷한 느낌으로 접근한 문제여서 감회가 새롭다.
https://www.acmicpc.net/problem/15649(15649번: N과 M(1))
예전에 풀었던 백준 사이트의 ‘N과 M’시리즈 문제가 이 로직을 구현하는 데 정말 많은 도움이 되었다.
알고리즘 풀이가 프로젝트에 도움이 되는 날이 올 줄이야…
백트래킹을 이용하는 것부터가 코드의 간결성이라는 장점이 있지만, 코드의 효율은 떨어진다는 단점을 가지고 있었다. 내부에서 함수 호출이 많이 발생할 경우, 도중에 게임이 멈춰버릴 수도 있는 상황도 충분히 발생하기에 해당 코드를 사용하기 위한 복잡도 계산을 꽤 열심히 했던 것으로 기억한다.
Q. 4가지의 숫자를 순서대로 배치하고, 사칙연산을 진행했을 때의 모든 경우의 수는?
- 4개의 숫자를 배치할 수 있는 모든 경우의 수 : 432*1=24가지
- 배치된 숫자에서 모든 사칙연산을 진행하는 모든 경우의 수 : 444=64가지
- 총경우의 수 : 24*64=최대 1536가지
애초에 4개의 수만을 사용하여 연산을 진행하기에 생각보다 적은 수의 연산이 진행되는 것을 파악하였고, 복잡도가 높아도 최대 연산 수는 2000도 넘지 않기에 해당 알고리즘을 사용하기로 하였다.
이후 해당 로직을 이용하여 테스트를 돌린 결과, 몇몇 결과에 대한 케이스를 잡지 못한 경우가 있다는 것을 알게 되었다. 로직 상의 에러를 잡기 위해 뭐가 문제였을까 별별 사람들을 붙잡고 코드 리뷰를 진행해보았고 그 이유를 곧 찾아냈다.
결과적으로 보았을 때, 해당 로직으로는 (ab)+(cd)와 같은 사칙연산상의 우선순위로만 나오는 정답에 대해서는 체크하지 않는다는 것을 알게 되었다.
이에 대한 예외처리를 진행하였고, 이후 정상적인 동작이 되는 것을 확인하였다.
const orderingException = (ordering) => {
//exception process
const orderOps = ["*", "/"];
for (let i1 = 0; i1 < 2; i1++) {
const [operOne, evalOne] = [
`(${ordering[0]}${orderOps[i1]}${ordering[1]})`,
eval(`(${ordering[0]}${orderOps[i1]}${ordering[1]})`),
];
if (evalOne > 0 && Number.isInteger(evalOne)) {
for (let i2 = 0; i2 < 2; i2++) {
const [operTwo, evalTwo] = [
`(${ordering[2]}${orderOps[i2]}${ordering[3]})`,
eval(`(${ordering[2]}${orderOps[i2]}${ordering[3]})`),
];
if (evalTwo > 0 && Number.isInteger(evalTwo)) {
const [resultOne, resultEvalOne] = [
`${operOne}+${operTwo}`,
eval(`${operOne}+${operTwo}`),
];
if (
!allCases.has(resultEvalOne) ||
(allCases.get(resultEvalOne).length > resultOne.length &&
String(resultEvalOne).length === 2)
)
allCases.set(resultEvalOne, resultOne); //init plus op
const [resultTwo, resultEvalTwo] = [
`${operOne}-${operTwo}`,
eval(`${operOne}-${operTwo}`),
];
if (resultEvalTwo > 0) {
//init minus op
if (
!allCases.has(resultEvalTwo) ||
(allCases.get(resultEvalTwo).length > resultTwo.length &&
String(resultEvalTwo).length === 2)
)
allCases.set(resultEvalTwo, resultTwo);
}
}
}
}
}
};
이를 고려하여 다시 경우의 수를 작성하면 다음과 같을 것이다
- 연산의 우선순위 상으로 따로 수행해야 하는 연산 : 222=8가지
- 총 연산 : 1536+8=최대 1544가지
💡 생각보다 적은 연산 수를 추후에 생각해보았을 때, 그냥 단순히 예외 8개를 입력시켜주면 코드가 더 깔끔해질 것 같다.
'개발 > 소프트웨어 마에스트로' 카테고리의 다른 글
| SWM에서 게임 개발로 살아남기(7. Novelists) (2) | 2022.11.30 |
|---|---|
| SWM에서 게임 개발로 살아남기(6. Deleterow) (0) | 2022.11.22 |
| SWM에서 게임 개발로 살아남기(4. Picoke) (0) | 2022.11.18 |
| SWM에서 게임 개발로 살아남기(3. 게임 데이터 수집) (0) | 2022.11.16 |
| SWM에서 게임 개발로 살아남기(2. 게임 기획) (2) | 2022.11.14 |