이전 내용과 이어집니다.
https://songmin9813.tistory.com/40(2. 데이터 전처리)
독립 변수의 개수도 적고, 데이터의 상관관계 또한 우상향 그래프를 그리고 있기에 단순 선형 회귀 모델을 이용한 ML 모델을 만들어보고자 한다.
모델을 만듦에 있어서 독립 변수는 distance, steps로, 종속 변수는 calories로 둔 채 최소 자승법을 이용한 회귀 분석을 진행한다.

우상단 R-squared 값이 0.786으로 약 78% 설명력을 보이고 있지만, distance와 steps의 p-value 값이 충분한 신뢰도를 보이고 있지 않다. (각각 0.982, 0.582) 이는 각 값이 서로를 설명할 수 있는 다중 공선성 문제라 판단했기에 p-value가 가장 높은 distance 변수를 제거 후 다시 분석을 진행하도록 한다.
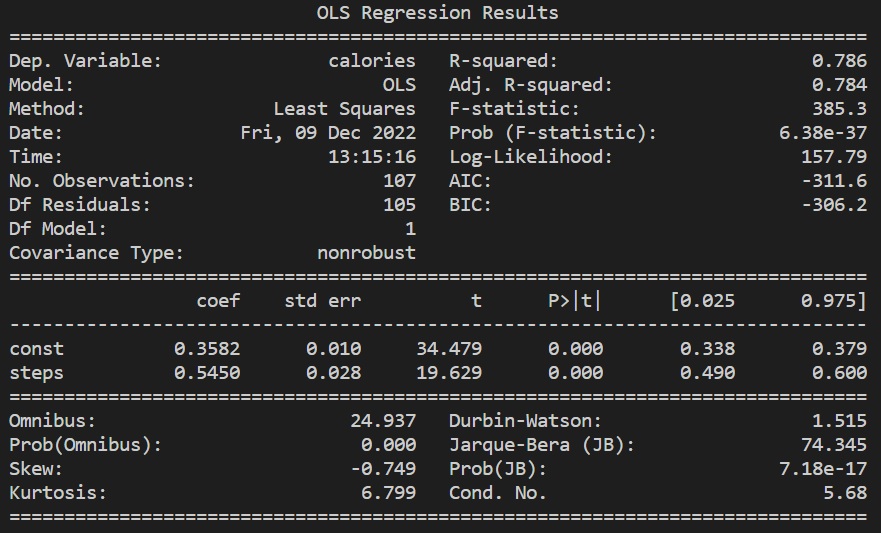
distacne 변수를 제거하였는대도 R-squared 값은 변하지 않았고, 되려 steps의 p-value가 현저히 낮아져 해당 변수로도 충분한 설명이 가능할 것이라 판단했다.
상기 두 지표를 이유로 steps 변수만을 이용하여 단순 선형 회귀 분석을 진행해 보도록 한다. 존재하는 데이터가 200개도 안 되는 소수의 데이터이기 때문에 훈련 데이터와 검증 데이터를 번갈아가면서 사용하는 K-Fold 교차 검증 방식을 이용하여 총 5번의 훈련을 진행했다.
소모 칼로리는 실수 영역이기 때문에 정확도 계산을 사용할 수 없기에 잔차 제곱합(MSE)을 이용한 비교를 진행하도록 한다. 아래의 사진은 모든 변수를 넣었을 때의 잔차가 표시된 그래프이다. 0에 가까울수록 적합이 잘 된 것이라 할 수 있다.

아래는 steps 변수만을 넣었을 때의 답과의 잔차가 표시된 그래프이다. 0에 가까울수록 적합이 잘 된 것이라 할 수 있다.

그래프 상으로는 유의미한 차이를 보이지 않았고, 잔차제곱합의 평균 또한 등락의 차이가 심하게 발생하지 않았다.

따라서 모델의 성능을 위하여 변수가 최소한으로 들어간 두 번째 모델을 사용하는 것이 바람직할 것이다.
부록 : 코드 전문
아래는 해당 프로그램을 작성하기 위한 코드의 전문이 수록되어 있다. 다른 환경에서 작동시키고 싶을 경우, PATH 내의 경로를 자신의 데이터 경로로 맞춰 설정하면 올바르게 작동할 것이다.
코드에 대한 설명은 주석으로 달아놨으니 추가적인 질문이나 피드백이 있다면 댓글 남겨놓으시라.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas.plotting import scatter_matrix
import statsmodels.api as sm
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
PATH = "파일저장경로"
def main():
calories=pd.read_csv(PATH+"/results_calories.txt",encoding="utf-8",sep=" ",names=["date","calories"],index_col="date")
distance=pd.read_csv(PATH+"/results_distance.txt",encoding="utf-8",sep=" ",names=["date","distance"],index_col="date")
steps=pd.read_csv(PATH+"/results_stpes.txt",encoding="utf-8",sep=" ",names=["date","steps"],index_col="date")
# 사전 정의된 경로를 바탕으로 csv 파일을 읽어옴
# csv 형식은 아니지만 구분자를 적절히 설정함으로 csv처럼 읽어오는 것이 가능했음
# 인덱스는 primary key인 date를 기준으로 인덱싱 작업을 거쳤다
fig=plt.figure()
ax1=fig.add_subplot(3,1,1)
ax2=fig.add_subplot(3,1,2)
ax3=fig.add_subplot(3,1,3)
ax1.plot(calories.loc[:"2021-04-30"])
ax1.axes.xaxis.set_visible(False)
ax1.set_title("calories") # subplot 하나 생성
ax2.plot(distance.loc[:"2021-04-30"])
ax2.axes.xaxis.set_visible(False)
ax2.set_title("distance") # subplot 하나 생성
ax3.plot(steps.loc[:"2021-04-30"])
ax3.axes.xaxis.set_visible(False)
ax3.set_title("steps") # subplot 하나 생성
plt.show()
df=calories.join(distance).join(steps)
print(df.info()) # 각각의 컬럼에 대하여 결측치 존재 여부 확인
df=calories.join(distance).join(steps)
df.plot()
plt.show() # 그냥 출력했을 때의 결과
normalization_df=(df-df.min())/(df.max()-df.min())
normalization_df.plot()
print(normalization_df.corr())
plt.show() # 정규화 진행 후 출력 결과
scatter_matrix(normalization_df)
plt.show() # 각각의 변수에 대한 산점도 그래프 형성
norm_drop_df=normalization_df[(normalization_df["steps"]!=0) | (normalization_df["distance"]!=0)]
# 거리나 걸음이 하나라도 0인 데이터가 있다면 삭제 후 반환
scatter_matrix(norm_drop_df)
plt.show()
# 이상치를 제외한 산점도 그래프 형성
drop_df=df[(df["steps"]!=0) | (df["distance"]!=0)]
# 정규화를 진행하지 않고 이상치만 제거만 df 생성
norm_x=drop_df.drop(['calories'],axis=1) # 독립변수를 만들기 위한 테이블
target=drop_df[["calories"]] # 타겟 변수는 소모 칼로리
x_data=sm.add_constant(norm_x,has_constant="add") # 최소자승법 사용을 위한 임시 변수 테이블 생성
multi_model=sm.OLS(target,x_data)
fitted_multi_model=multi_model.fit()
print(fitted_multi_model.summary()) # 적합 후 요약 생성
x_data2=sm.add_constant(norm_x.drop(["distance"],axis=1),has_constant="add")
# distance 변수를 삭제한 후 상기 방법과 같은 방법으로 최소자승법 시행
multi_model2=sm.OLS(target,x_data2)
fitted_multi_model2=multi_model2.fit()
print(fitted_multi_model2.summary())
X=x_data #상수항이 추가된 2개의 데이터
y=target
mse_history=[] # MSE 값이 들어갈 리스트
kf=KFold(n_splits=5,shuffle=True,random_state=30)
for train_index,test_index in kf.split(X):
# K fold 검증의 스플릿 횟수는 5번. 이에 맞춰 각 셋을 분할한다.
X_train,X_test=X.iloc[train_index],X.iloc[test_index]
y_train,y_test=y.iloc[train_index],y.iloc[test_index]
reg_model=sm.OLS(y_train,X_train)
fitted=reg_model.fit() # 회귀모델 적합
y_pred=fitted.predict(X_test)
plt.plot(np.array(y_test["calories"]-y_pred))
# 정답과 예측값의 잔차를 그래프로 출력
mse_history.append(mean_squared_error(y_true=y_test,y_pred=y_pred))
print("변수 2개를 넣었을 때의 평균 잔차제곱합 :",np.mean(mse_history))
plt.title("Input 2 Variables")
plt.show()
X=x_data2 #상수항이 추가된 2개의 데이터
# 모든 시행은 동일하게 하되, X의 값만 다르게 하여 출력한다.
y=target
mse_history=[]
kf=KFold(n_splits=5,shuffle=True,random_state=30)
for train_index,test_index in kf.split(X):
#print(train_index,test_index)
X_train,X_test=X.iloc[train_index],X.iloc[test_index]
y_train,y_test=y.iloc[train_index],y.iloc[test_index]
reg_model=sm.OLS(y_train,X_train)
fitted=reg_model.fit()
y_pred=fitted.predict(X_test)
plt.plot(np.array(y_test["calories"]-y_pred))
mse_history.append(mean_squared_error(y_true=y_test,y_pred=y_pred))
print("변수 1개를 넣었을 때의 평균 잔차제곱합 :",np.mean(mse_history))
plt.title("Input 1 Variable")
plt.show()
if __name__ == '__main__': # main()
main()
추가적으로 python 파일과 분석에 사용한 3개의 데이터도 공유하니 심심하면 직접 실행해보는 것도 좋을 것 같다.
pw : songmin9813
'개발 > 데이터 분석' 카테고리의 다른 글
| 배틀그라운드 유저 데이터 분석해보기 1. 프로세스 수립 (1) | 2023.01.13 |
|---|---|
| Tableau 대시보드 제대로 활용하기 - 콘텐츠 구성편 (2) | 2023.01.11 |
| 도보에 따른 칼로리 소모량 분석해보기 2. 데이터 전처리 (0) | 2023.01.07 |
| 도보에 따른 칼로리 소모량 분석해보기 1. 데이터 인사이트 (2) | 2023.01.05 |
| Analytic SQL 5. 이동 평균(Moving Average)과 유의 사항 (0) | 2023.01.05 |